What is Inverse Molecular Design?
Discovering materials with optimum properties is a long-term dream for both experimental and theoretical researchers. Historically, researchers use the approach of “trial and error” to find new materials with desired properties. Owing to the development in modern theoretical and computational chemistry (e.g., density functional theory), predicting molecular properties using accurate and efficient quantum chemistry methods becomes more and more practical. As a consequence, inverse molecular design is emerged as an attractive computational approach to attack the challenges in materials discovery.
Inverse molecular design is a general term for the strategies in molecular design, relative to the strategy of direct design. In direct design, a new molecule is proposed first, and then the molecular property is computed or tested to check its feasibility. In contrast, inverse molecular design aims to search for the optimum points in the hypersurface of the property-structure relationship, and then map out the molecular structures at the optimum points. Hence, using the idea of inverse molecular design could significantly to enhance the successful rate of molecular design and save the cost in materials discovery.
Inverse molecular design has been implemented as an optimization problem in theory,
i.e. searching for the optimum chemical structures with the aid of optimization algorithms.
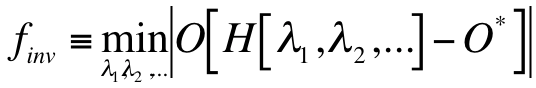Here, 
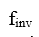is a notation for the operation of inverse molecular design. O denotes a molecular property (an observable),
which is a functional of the Hamiltonian H.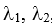 
, and … are a set of variables of the Hamiltonian,
through which different molecular structures are represented.
O* denotes the target molecular property, e.g. a maximum point of the molecular property. Notation ‘min’ means adapting different optimization algorithms for minimizing the absolute value of .
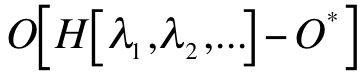Thus, 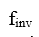aims to find a particular set of variables 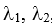, …(and thus a molecular structure) that shows the closest matching to the target molecular property.
In the molecular structure space, the Hamiltonian variables are associated with the atoms types and their connectivity. With the choice of the Hamiltonian variables, i.e. the way of varying molecular structures in a chemical structure space, different optimization algorithms (including stochastic and deterministic algorithms) have been adapted for inverse molecular design methods. In the following, we will first review the optimization algorithms based on discrete molaecule objects such as genetic algorithm, Monte Carlo, and neural network. And then, we describe an emergent approach of using deterministic algorithms to search for optimum molecules in alchemical space, named linear combination of atomic potential (LCAP). In particular, we will apply LCAP in the tight-binding framework, which could provide a fast way for molecule search. Finally, we will review the applications of the TB-LCAP in the optical materials and dye-sensitized solar cells. Novel materials have been proposed by TB-LCAP and verified by experiments. Due to the low computational cost of tight-binding electronic structure theories, we anticipate the TB-LCAP will be a promising the inverse molecular design methods for attacking challenges in materials discovery such as catalysts design.